
Part 1: U+237C ⍼ RIGHT ANGLE WITH DOWNWARDS ZIGZAG ARROW
Part 2: update: U+237C ⍼ angzarr;
This is part 3.
Part 4: U+237C ⍼ is (also) S9576 ⍼
Many thanks to Alicia Chilcott and Sophie Hawkey-Edwards at St Bride for their help.
I got the chance to visit St. Bride Library in London, where they held several Monotype catalogues, including the one containing ⍼. Here, I’ll catalogue the catalogues I took a look at. But first, some typesetting terminology to get things sorted.
Terminology
- Glyphs. This is what Unicode uses to refer to the abstract symbol itself, independent of implementation (e.g. the codepoints that make it up).
- Punches. The physical existence of a glyph begins as a punch, cut mirrored and in relief into a hard metal.
- Matrices. The punch is then struck into a soft metal to create a matrix, which is used as a mould. Presumably glyphs are catalogued by their matrices and assigned matrix numbers for printers to request.
- Types and sorts. A metal type, or sort, is cast from the matrix and used for printing. While type seems to only refer to the physical metal block, sort is also metonymically used to refer to the glyph that it prints, leading to catalogues of sorts.
Catalogues
At St Bride Library, I looked at a total of six documents:
- List of Monotype Founts and Tables of Special Sorts at the University Press, Oxford, June 1935.
- List of Monotype Founts and Special Sorts at the University Press, Oxford, October 1976.
- “Monotype” Special Sorts: Specimens of Arbitrary Characters not included in ordinary sets of Matrices, 1932. Also in Alembic Press’ collection (although dated as 1931).
- ‘Monotype’ Mathematical Sorts List, selected and compiled by Arthur Phillips, 1957. Also in Alembic Press’ collection (although dated as 1956).
- An Informal Addendum to the Mathematical Sorts List, 1957.
- List of mathematical characters, which includes ‘Monotype’ 4-line Mathematics Series 569 & L231 and ‘Monophoto’ Times Mathematics Series 569B & L231B, 1972. Also in the Morison Collection; and a document containing only Series 569 appears to be listed in Alembic Press’ collection, dated 1967.
List of Monotype Founts
The 1935 and 1976 lists are booklets of, I think, legal-paper size, with the latter seemingly an update of the former, being about twice as thick. They contain lists of fonts and lists of special sorts, such as mathematical sorts and special borders. Although fairly comprehensive for ordinary mathematical use, the mathematical sorts sections are pretty sparse in comparison to the mathematics-specific catalogues.
 Front cover of the 1935 edition
Front cover of the 1935 edition
 Excerpt of mathematical signs
Excerpt of mathematical signs
 Front cover of the 1976 edition
Front cover of the 1976 edition
 Excerpt of mathematical signs
Excerpt of mathematical signs
Monotype Special Sorts
Now this is an enormous tome. It appears to attempt to catalogue every single special sort made up to 1932, including the S series of sorts ranging from matrix numbers S1 to S3998, with plenty of blank entries left presumably to be updated as more were made. A number of entries appear to be hand-corrected or glued on later.
 Exterior of tome
Exterior of tome
 First page
First page
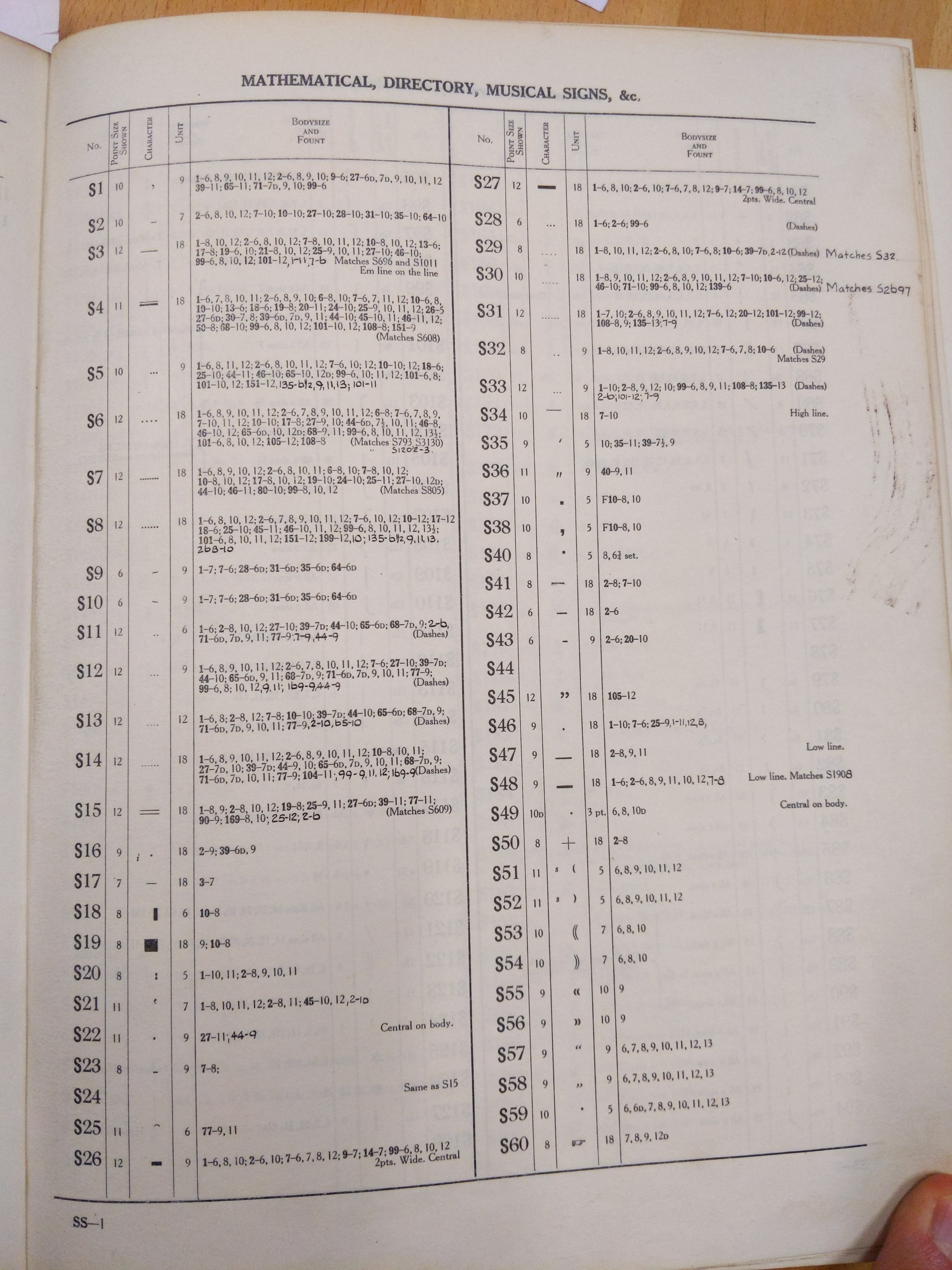 Beginning of S series of sorts
Beginning of S series of sorts
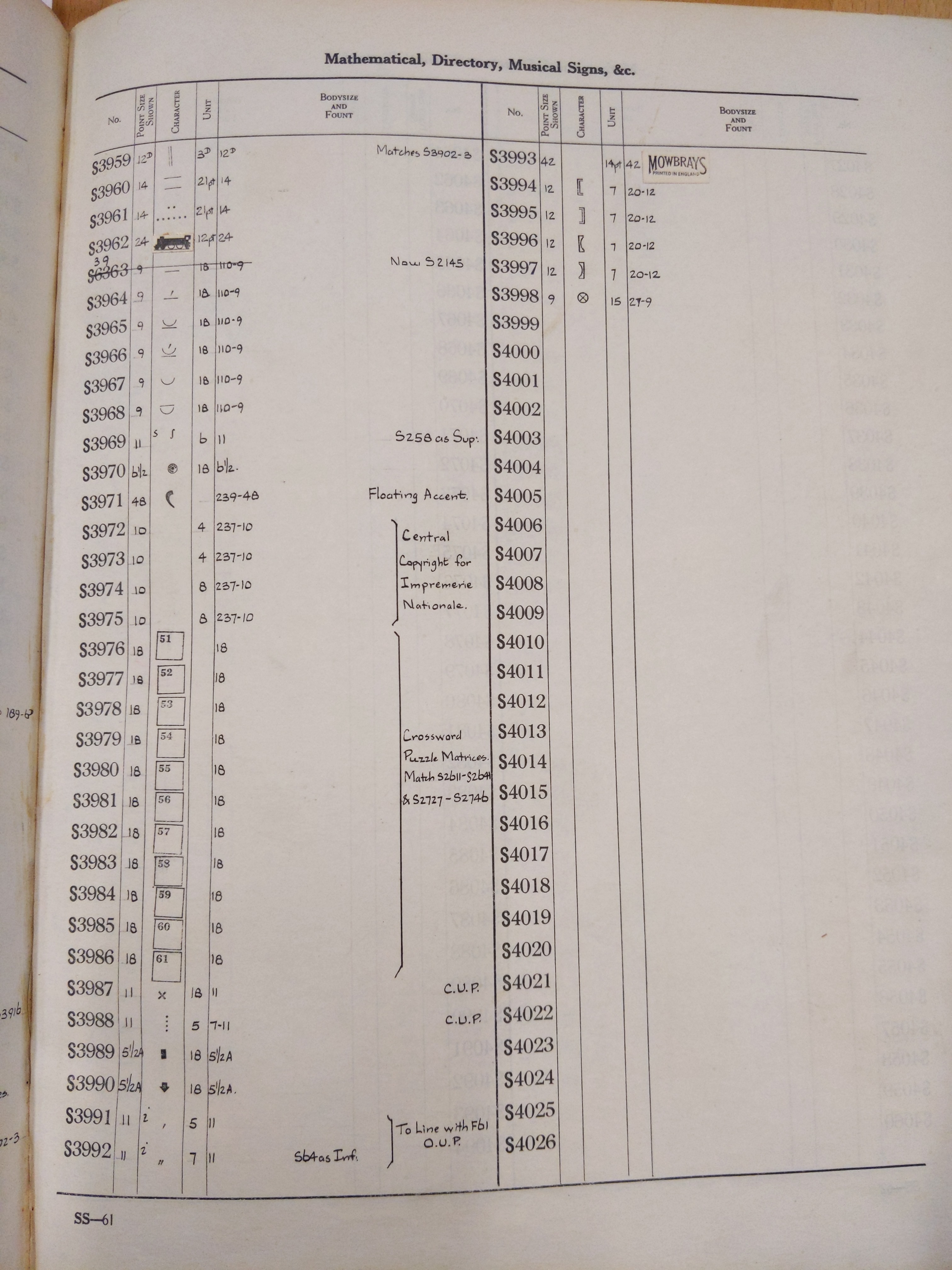 End of S series of sorts
End of S series of sorts
What was surprising to me was that sorts made specifically for company logos are catalogued and included as special sorts!
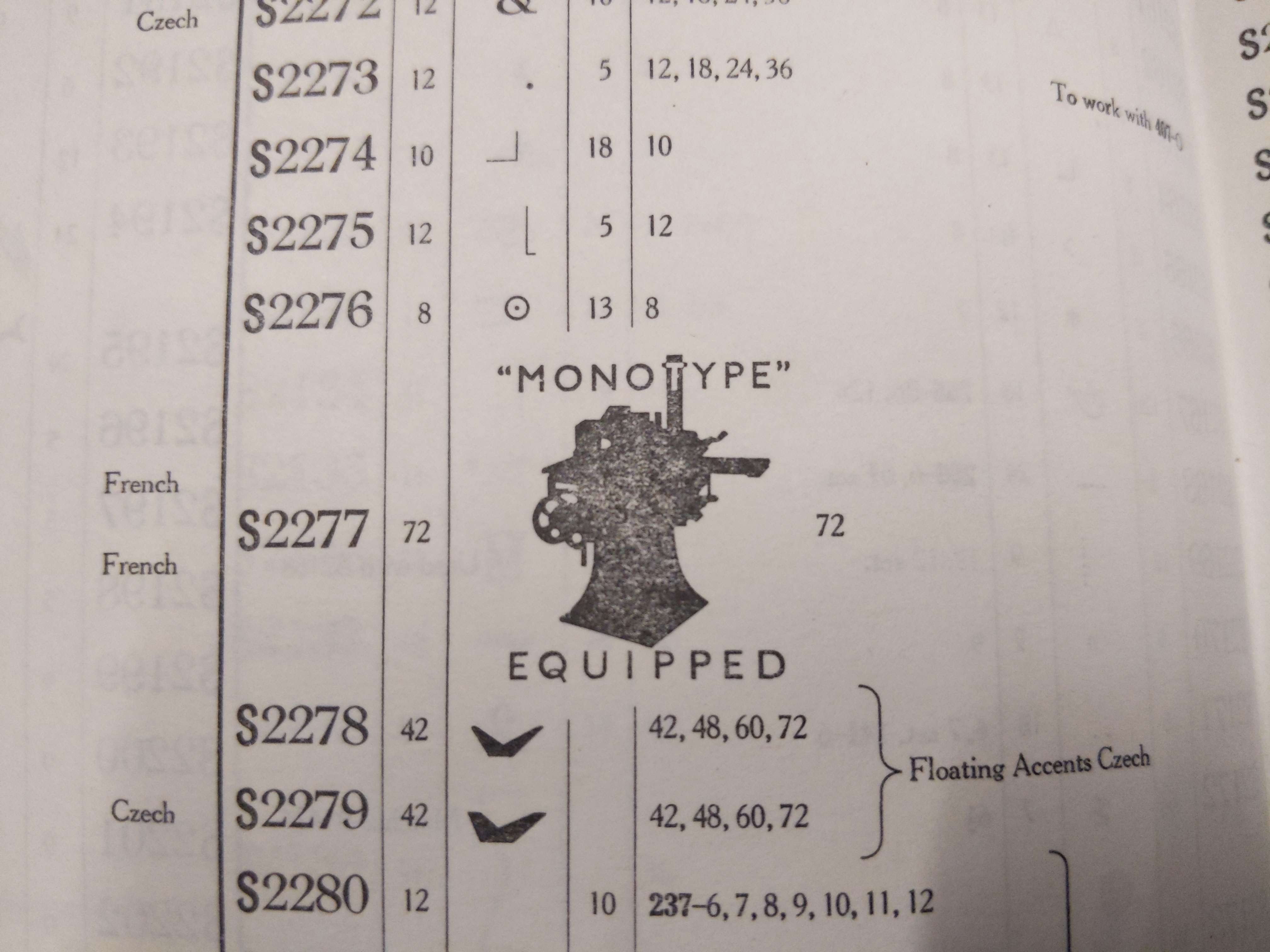 "Monotype" equipped
"Monotype" equipped
 Borzoi Books
Borzoi Books
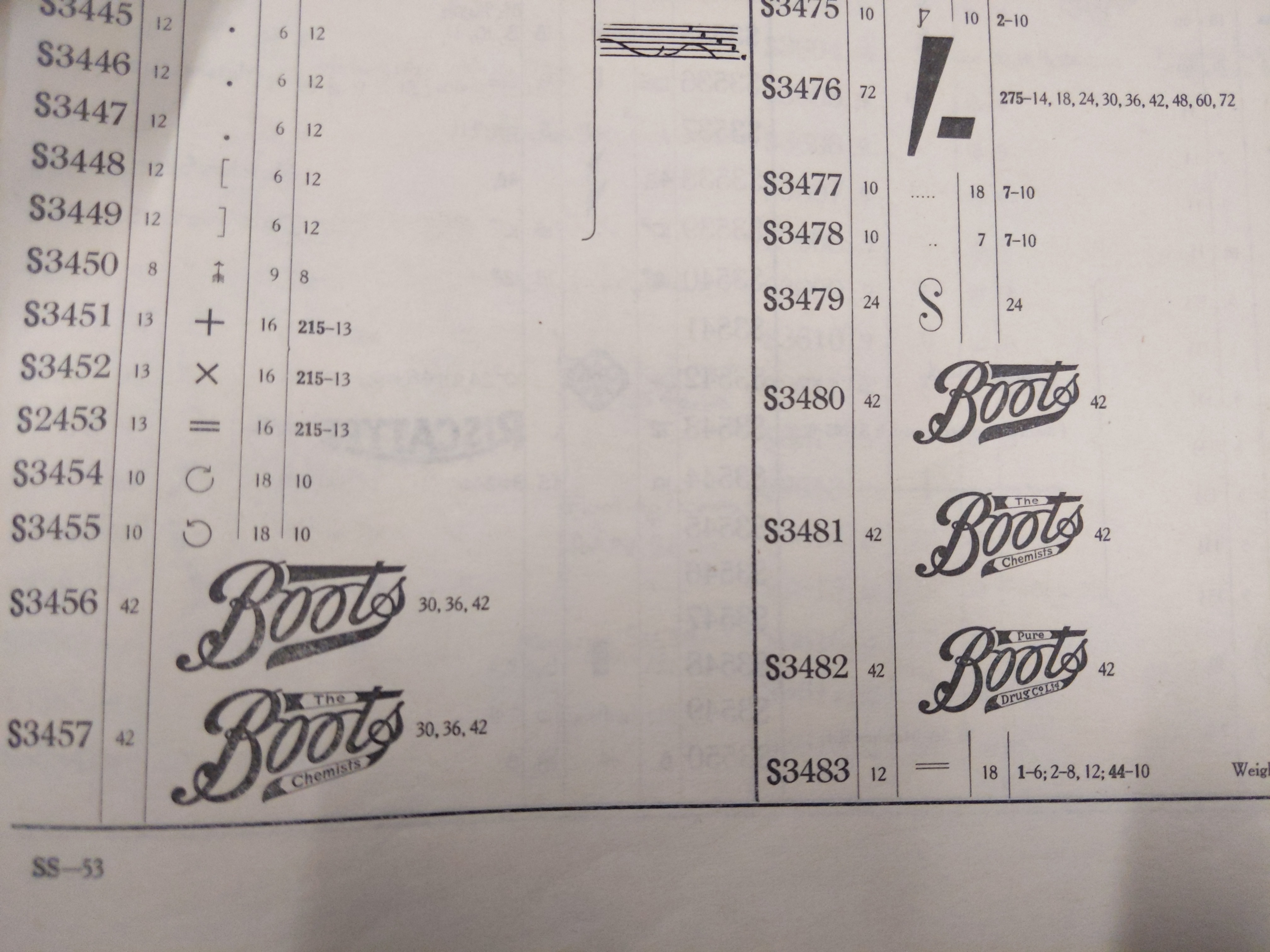 Boots
Boots
 "His Master's Voice"
"His Master's Voice"
 Various other logos
Various other logos
 A sentry guard
A sentry guard
 Some union jacks
Some union jacks
 ???
???
Monotype Mathematical Sorts List
I really like this 1957 booklet because it’s a very well-curated selection, with plenty of explanatory text and descriptions of what each sort means when available. The sorts are sorted not by matrix number, but rather by their intended semantic meanings. It apparently is a reference book which complements volume 40, issue number 4 of the Monotype Recorder, Setting Mathematics, with a glossary of mathematical terms and nomenclature of signs, also written by Arthur Phillips, from the winter of 1956. The “Names or descriptions of Mathematical Signs” on page 26 can also be found in the Sorts List.
 Front cover, along with the inserted addendum
Front cover, along with the inserted addendum
 First page
First page
 Excerpt about the special signs and symbols
Excerpt about the special signs and symbols
This booklet comes with an addendum as a slip of paper, containing a single poem by Arthur Phillips titled Mathematical Sorts in Continuous Creation which, with the power of Unicode, I transcribe below, together with its reading.
 Front and back covers
Front and back covers
 The poem, along with an editor's note
The poem, along with an editor's note
A ′ ° of ↻ sense,
∈ doubt,
÷ ∞
Will help the theorist out.
So this →
Which ⇛ creation
And ↔, I'm told,
A transfinite ∼.
A ⧧
Is ≃
The ∜ of a ⊕
(It means the same to you);
So ⪪, so >,
≺ a 𝑝∣𝑞
The =
Of Bondi, 𝐴𝑢 and Hoyle.
|
A prime degree of clockwise sense,
An element of doubt,
Divided by infinity
Will help the theorist out.
So this tends to the limit
Which converges to creation
And mutually implies, I'm told,
A transfinite negation.
A logical diversity
Is asymptotic to
The fourth root of a direct sum
(It means the same to you);
So "smaller than", so "greater than"
Contains a joint denial,
The logical identity
Of Bondi, Gold and Hoyle.
|
List of Mathematical Characters
And finally, here we have once again the 1972 list of mathematical characters, including series L231 containing ⍼, which is bound together with the original list rather than collected alongside as looseleaf. What I found the most interesting was the preamble given before the list, in particular the paragraphs describing the difference between series 569 and L231.
 Front cover
Front cover
 First page
First page
 The page containing ⍼ S16139
The page containing ⍼ S16139
It should be understood that Series 569 contains only those characters which are (a) mathematical and (b) recognised internationally. We are periodically asked to supply characters which do not meet these conditions. In order to meet such requests we have therefore provided the supplementary fount L231.
L213-10 pt has the same Group numbers, and conforms with Series 569 in all respect of matrix manufacture, casting and usage. However, we do suggest that customers, on finding that a particular character they require is made in L231, should, nevertheless, still endeavour to persuade their customer or author to use normal notation from Series 569. We shall be only too pleased to provide any relevant data regarding why the character has been made in the L231 category, should this be requested.
The implication is that, in 1972 at least, Monotype did retain records for the meanings of specials sorts including those in L231! I haven’t found any evidence of updated tomes of Monotype Special Sorts, so I imagine that they would be internal documents rather than publications. Unfortunately, such documents would probably be in the now-defunct Type Archive, whose materials are in storage in the Science Museum Group’s National Collections Centre.


