I’ve wanted to write an informal (but technical!) post about my current research in progress on Stratified Type Theory (StraTT), but we’ve been occupied with writing up a paper draft for submission to CPP 2024, then writing a talk for NJPLS Nov 2023, then being rejected from CPP, then I’ve just been randomly distracted for two weeks but I’m so back now.
That paper draft along with the supplementary material will have all the details, but I’ve decided that what I want to focus on in this post is all the other variations on the system we’ve tried that are either inconsistent or less expressive. This means I won’t cover a lot of motivation or examples (still a work in progress), or mention any metatheory unless where relevant; those can be found in the paper. Admittedly, these are mostly notes for myself, and I go at a pace that sort of assumes enough familiarity with the system to be able to verify well-typedness mentally, but this might be interesting to someone else too.
Contents
The purpose of StraTT is to introduce a different way of syntactically dealing with type universes, and the premise is to take a predicative type theory with a universe hierarchy, and instead of stratifying universes by levels, you instead stratify typing judgements themselves, a strategy inspired by Stratified System F. This means level annotations appear in the shape of the judgement , where is a term, is a type, is a level, and is a list of declarations .
Here are the rules for functions.
Function introduction and elimination are as expected, just with level annotations sprinkled in; the main difference is in the dependent function type. Just as the stratification of universes into a hierarchy serves to predicativize function types, so too does stratification of judgements, here done explicitly through the constraint . This means that if you have a function of type at level , you can’t pass that same type to the function as the type argument, since its level is too big.
Type in type
Because universes no longer have levels, we do in fact have a type-in-type rule for any . But this is okay! The judgement stratification prevents the kind of self-referential tricks that type-theoretic paradoxes typically take advantage of. The simplest such paradox is Hurkens’ paradox, which is still quite complicated, but fundamentally involves the following type.
For the paradox to work, the type argument of a function of type needs to be instantiated with itself, but stratification prevents us from doing that, since .
Cumulativity
Cumulativity is both normal to want and possible to achieve. There are two possible variations to achieve it: one adds cumulativity to the variable rule and leaves conversion alone.
Alternatively, the variable rule can be left alone, and cumulativity integrated into the conversion rule.
Either set is admissible in terms of the other. I’m not going to tell you which one I’ve picked.
Syntactic level annotations
Level annotations are tedious and bothersome. Can we omit them from function types?
The answer is no. Doing so allows us to derive exactly the inconsistency we set out to avoid. Suppose our function type domains aren’t annotated with levels, and let . Then by cumulativity, we can raise its level, then apply it to .
The strict level constraint is still there, since the level of remains strictly smaller than that of . But without the annotation, the allowed level of the domain can rise as high as possible, yet still within the constraint, via cumulativity.
Displacement
The formalism of StraTT also supports a global context which consists of a list of global definitions , where is a constant of type and body at level . Separately from cumulativity, we have displacement, which is based on Conor McBride’s notion of “crude-but-effective stratification”: global definitions are defined with fixed, constant levels, and then uniformly incremented as needed. This provides a minimalist degree of code reusability across levels without actually having to introduce any sort of level polymorphism. Formally, we have the following rules for displaced constants and their reduction behaviour that integrates both displacement and cumulativity.
The metafunction recursively adds to all levels and displacements in a term; below are the two cases where the increment actually has an effect.
As an example of where displacement is useful, we can define a function that takes an argument of the displaced type , which now takes a type argument at level , so is then well typed.
Floating (nondependent) functions
You’ll notice that I’ve been writing nondependent functions with arrows but without any level annotations. This is because in StraTT, there’s a separate syntactic construct for nondependent functions which behaves just like functions but no longer has the strict stratification restriction.
Removing the restriction is okay for nondependent function types, because there’s no risk of dependently instantiating a type variable in the type with the type itself.
These are called floating functions because rather than being fixed, the level of the domain of the function type “floats” with the level of overall function type (imagine a buoy bobbing along as the water rises and falls). Specifically, cumulativity lets us derive the following judgement.
Unusually, if we start with a function at level that takes some at level , we can use at level as if it now takes some at a higher level . The floating function is covariant in the domain with respect to the levels! Typically functions are contravariant or invariant in their domains with respect to the ambient ordering on types, universes, levels, etc.
But why floating functions?
Designing StraTT means not just designing for consistency but for expressivity too: fundamentally revamping how we think about universes is hardly useful if we can’t also express the same things we could in the first place.
First, here’s an example of some Agda code involving self-applications of identity functions in ways such that universe levels are forced to go up to in a nontrivial manner (i.e. not just applying bigger and bigger universes to something). Although I use universe polymorphism to define , it isn’t strictly necessary, since all of its uses are inlineable without issue.
{-# OPTIONS --cumulativity #-}
open import Level
ID : ∀ ℓ → Set (suc ℓ)
ID ℓ = (X : Set ℓ) → X → X
𝟘 = zero
𝟙 = suc zero
𝟚 = suc 𝟙
𝟛 = suc 𝟚
-- id id
idid1 : ID 𝟙 → ID 𝟘
idid1 id = id (ID 𝟘) (λ x → id x)
-- id (λid. id id) id
idid2 : ID 𝟚 → ID 𝟘
idid2 id = id (ID 𝟙 → ID 𝟘) idid1 (λ x → id x)
-- id (λid. id (λid. id id) id) id
idid3 : ID 𝟛 → ID 𝟘
idid3 id = id (ID 𝟚 → ID 𝟘) idid2 (λ x → id x)
In , to apply to itself, its type argument needs to be instantiated with the type of , meaning that the level of the on the left needs to be one larger, and the on the right needs to be eta-expanded to fit the resulting type with the smaller level. Repeatedly applying self-applications increases the level by one each time. I don’t think anything else I can say will be useful; this is one of those things where you have to stare at the code until it type checks in your brain (or just dump it into the type checker).
In the name of expressivity, we would like these same definitions to be typeable in StraTT. Suppose we didn’t have floating functions, so every function type needs to be dependent. This is the first definition that we hope to type check.
The problem is that while expects its second argument to be at level , the actual second argument contains itself, which is at level , so such a self-application could never fit! And by stratification, the level of the argument has to be strictly smaller than the level of the overall function, so there’s no annotation we could fiddle about with to make fit in itself.
What floating functions grant us is the ability to do away with stratification when we don’t need it. The level of a nondependent argument to a function can be as large as the level of the function itself, which is exactly what we need to type check this first definition that now uses floating functions.
The corresponding definitions for and will successfully type check too; exercise for the reader.
When do functions float?
I’ve made it sound like all nondependent functions can be made to float, but unfortunately this isn’t always true. If the function argument itself is used in a nondependent function domain, then that argument is forced to be fixed, too. Consider for example the following predicate that states that the given type is a mere proposition, i.e. that all of its inhabitants are indistinguishable.
If were instead assigned the floating function type at level , the type argument being at level would force the level of to also be , which would force the overall definition to be at level , which would then make be at level , and so on.
Not only are not all nondependent functions necessarily floating, not all functions that could be floating necessarily need to be nondependent, either. I’m unsure of how to verify this, but I don’t see why function types like the identity function type can’t float; I can’t imagine that being exploited to derive an inconsistency. The fixed/floating dichotomy appears to be independent of the dependent/nondependent dichotomy, and matching them up only an approximation.
Restriction lemma
Before I move on to the next design decision, I want to state and briefly discuss an important lemma used in our metatheory. We’ve proven type safety (that is, progress and preservation lemmas) for StraTT, and the proof relies on a restriction lemma.
Definition: Given a context and a level , the restriction discards all declarations in of level strictly greater than .
Lemma [Restriction]: If and , then and .
For the lemma to hold, no derivation of can have premises whose level is strictly greater than ; otherwise, restriction will discard those necessary pieces. This lemma is crucial in proving specifically the floating function case of preservation; if we didn’t have floating functions, the lemma isn’t necessary.
Relaxed levels
As it stands, StraTT enforces that the level of a term’s type is exactly the level of the term. In other words, the following regularity lemma is provable.
Lemma [Regularity]: If , then .
But what if we relaxed this requirement?
Lemma [Regularity (relaxed)]: If , then there is some such that .
In such a new relaxed StraTT (RaTT), the restriction lemma is immediately violated, since is a well-formed context, but isn’t even well scoped. So a system with relaxed levels that actually makes use of the relaxation can no longer accommodate floating functions because type safety won’t hold.
However, the dependent functions of RaTT are more expressive: the self-application can be typed using dependent functions alone! First, let’s pin down the new rules for our functions.
Two things have changed:
- The domain type can now be typed at the larger level rather than at the argument level ; and
- There’s no longer a restriction between the argument level and the function body level .
Since the premise still exists in the type formation rule, we can be assured that a term of type still can’t be applied to itself and that we still probably have consistency. Meanwhile, the absence of in the function introduction rule allows us to inhabit, for instance, the identity function type , where the level annotations no longer match.
Expressivity and inexpressivity
These rules let us assign levels to the self-application as follows.
Although the type of must live at level , the term can be assigned a lower level . This permits the self-application to go through, since the second argument of demands a term at level . Unusually, despite the second being applied to a type at level , the overall level of the second argument is still because quantification over arguments at higher levels is permitted.
Despite the apparently added expressivity of these new dependent functions, unfortunately they’re still not as expressive as actually having floating functions. This was something I discovered while trying to type check Hurkens’ paradox and found that fewer definitions were typeable. I’ve attempted to isolate the issue a bit by revealing a similar problem when working with CPS types. Let’s first look at some definitions in the original StraTT with floating functions.
translates a type to its answer-polymorphic CPS form, and translates a term into CPS. does the opposite and runs the computation with the identity continuation to yield a term of the original type. is a proposition we might want to prove about a given type and a computation of that type in CPS: passing as the continuation for our computation (as in ) to get another computation should, when run, yield the exact same result as running the computation directly.
By careful inspection, everything type checks. Displacements needed are in and on the type of the computation . This displacement raises the level of the answer type argument of so that the type can be instantiated with . Consequently, we also need to displace the that runs the displaced computation on the right-hand side of . Meanwhile, left-hand shouldn’t be displaced because it runs the undisplaced computation returned by .
Now let’s try to do the same in the new RaTT without floating functions. I’ll only write down the definition of and , and inline in the latter.
This is a little more difficult to decipher, so let’s look at what the types of the different pieces of are.
- has type from displacing .
- The second argument of must have type from instantiating with . This is also the type of .
- The types of the arguments , , and of the second argument are , , and from expanding .
- is ill typed because has level while takes an at level .
To fix this, we might try to increase the level annotation on in the definition of so that can accommodate . But doing so would also increase the level annotation on in the displaced type of to , meaning that is still too large to fit into . The uniformity of the displacement mechanism means that if everything is annotated with a level, then everything moves up at the same time. Previously, floating functions allowed us to essentially ignore increasing levels due to displacement, but also independently increase them via cumulativity.
Of course, we could simply define a second definition with a different level, i.e. for the level that we need, but then to avoid code duplication, we’re back at needing some form of level polymorphism over .
Level polymorphism
So far, I’ve treated level polymorphism as if it were something unpleasant to deal with and difficult to handle, and this is because level polymorphism is unpleasant and difficult. On the useability side, I’ve found that level polymorphism in Agda muddies the intent of the code I want to write and produces incomprehensible type errors while I’m writing it, and I hear that universe polymorphism in Coq is a similar beast. Of course, StraTT is still far away from being a useable tool, but in the absence of more complex level polymorphism, we can plan and design for more friendly elaboration-side features such as level inference.
On the technical side, it’s unclear how you might assign a type and level to something like , since essentially quantifies over derivations at all levels. We would also need bounded quantification from both ends for level instantiations to be valid. For instance, requires that the level of the type of the domain be strictly greater than , so the quantification is ; and flipping the levels, would require . While assigning a level to a quantification bounded above is easy (the level of the second type above can be ), assigning a level to a quantification bounded below is as unclear as assigning one to an unbounded quantification.
At this point, we could either start using ordinals in general for our levels and always require upper-bounded quantification whose upper bound could be a limit ordinal, or we can restrict level quantification to prenex polymorphism at definitions, which is roughly how Coq’s universe polymorphism works, only implicitly, and to me the more reasonable option:
We believe there is limited need for […] higher-ranked universe polymorphism for a cumulative universe hierarchy.
― Favonia et al. (2023)
With the second option, we have to be careful not to repeat the same mistakes as Coq’s universe polymorphism. There, by default, every single (implicit) universe level in a definition is quantified over, and every use of a definition generates fresh level variables for each quantified level, so it’s very easy (albeit somewhat artificial) to end up with exponentially-many level variables to handle relative to the number of definitions. On the other hand, explicitly quantifying over level variables is tedious if you must instantiate them yourself, and it’s tricky to predict which ones you really do want to quantify over.
Level polymorphism is clearly more expressive, since in a definition of type for instance, you can instantiate and independently, whereas displacement forces you to always displace both by the same amount. But so far, it’s unclear to me in what scenarios this feature would be absolutely necessary and not manageable with just floating functions and futzing about with the level annotations a little.
What’s in the paper?
The variant of StraTT that the paper covers is the one with stratified dependent functions, nondependent floating functions, and displacement. We’ve proven type safety, mechanized a model of StraTT without floating functions (but not the interpretation from the syntax to the semantics), and implemented StraTT extended with datatypes and level/displacement inference.
The paper doesn’t yet cover any discussion of RaTT with relaxed level constraints. I’m still deliberating whether it would be worthwhile to update my mechanized model first before writing about it, just to show that it is a variant that deserves serious consideration, even if I’ll likely discard it at the end. The paper doesn’t cover any discussion on level polymorphism either, and if I don’t have any more concrete results, I probably won’t go on to include it.
It doesn’t have to be for this current paper draft, but I’d like to have a bit more on level inference in terms of proving soundness and completeness. Soundness should be evident (we toss all of the constraints into an SMT solver), but completeness would probably require some ordering on different level annotations of the same term such that well-typedness of a “smaller” annotation set implies well-typedness of a “larger” annotation set, formalizing the inference algorithm, then showing that the algorithm always produces the “smallest” annotation set.
Summary
- Typing derivations are stratified by levels
- Dependent functions quantify over strictly lower types
- Floating functions use cumulativity to raise domain levels
- Displacement enables code reuse through uniformly incrementing levels
- Allowing type levels to be larger than term levels breaks type safety for floating functions
- Dependent functions and displacement alone are less expressive than also having floating functions
- Level polymorphism is still an open question that I’d rather not include
]]>
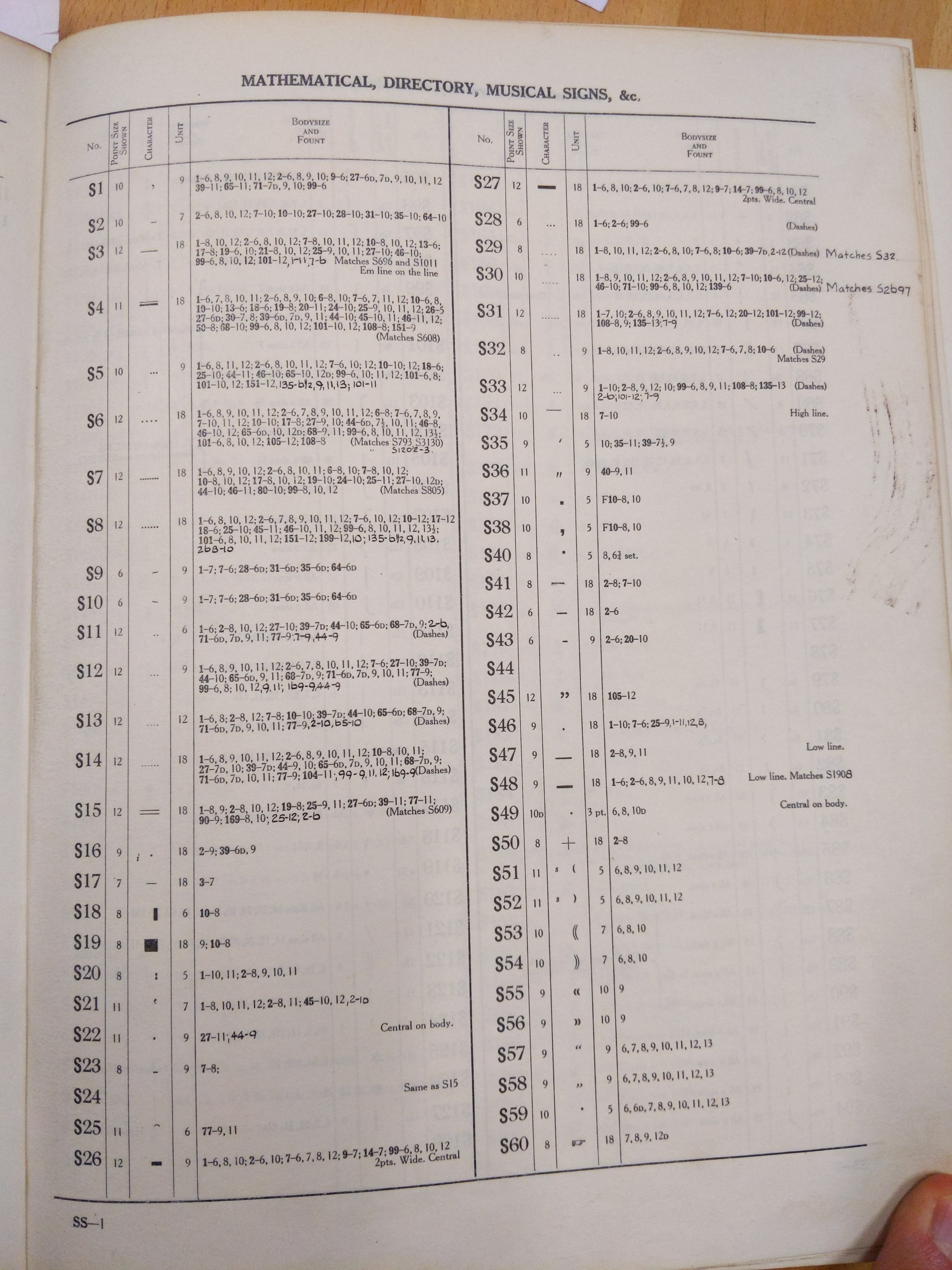
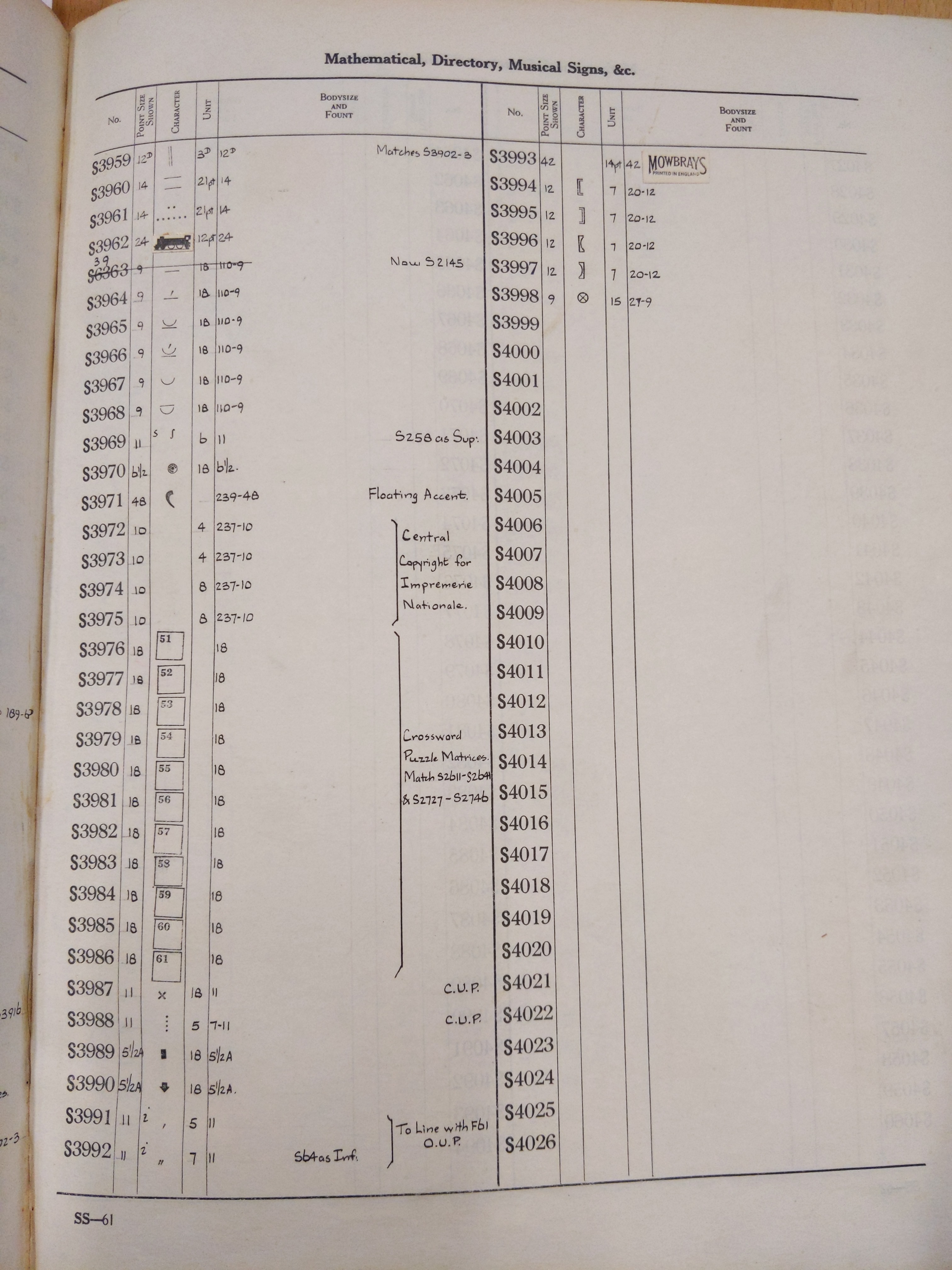
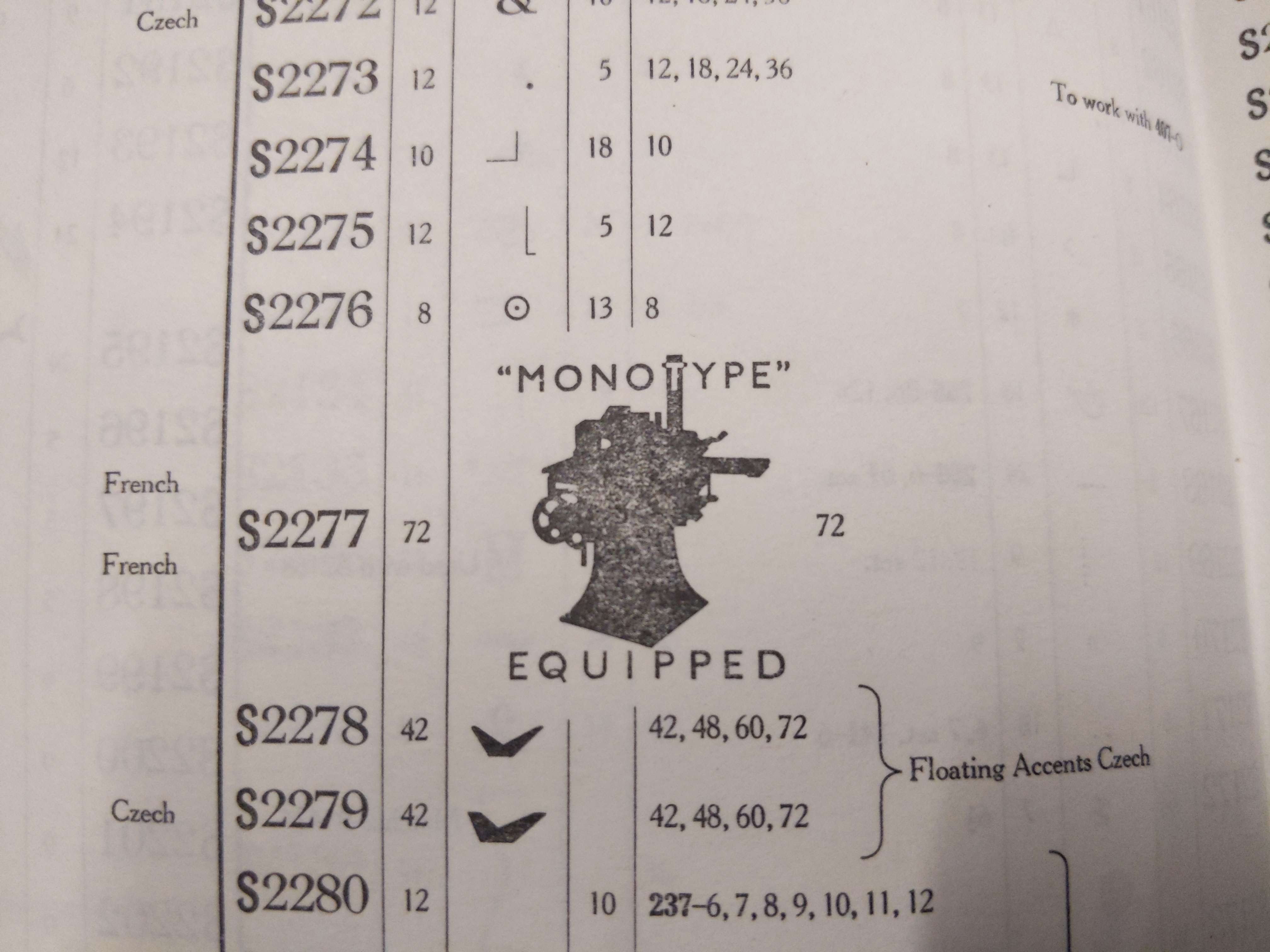
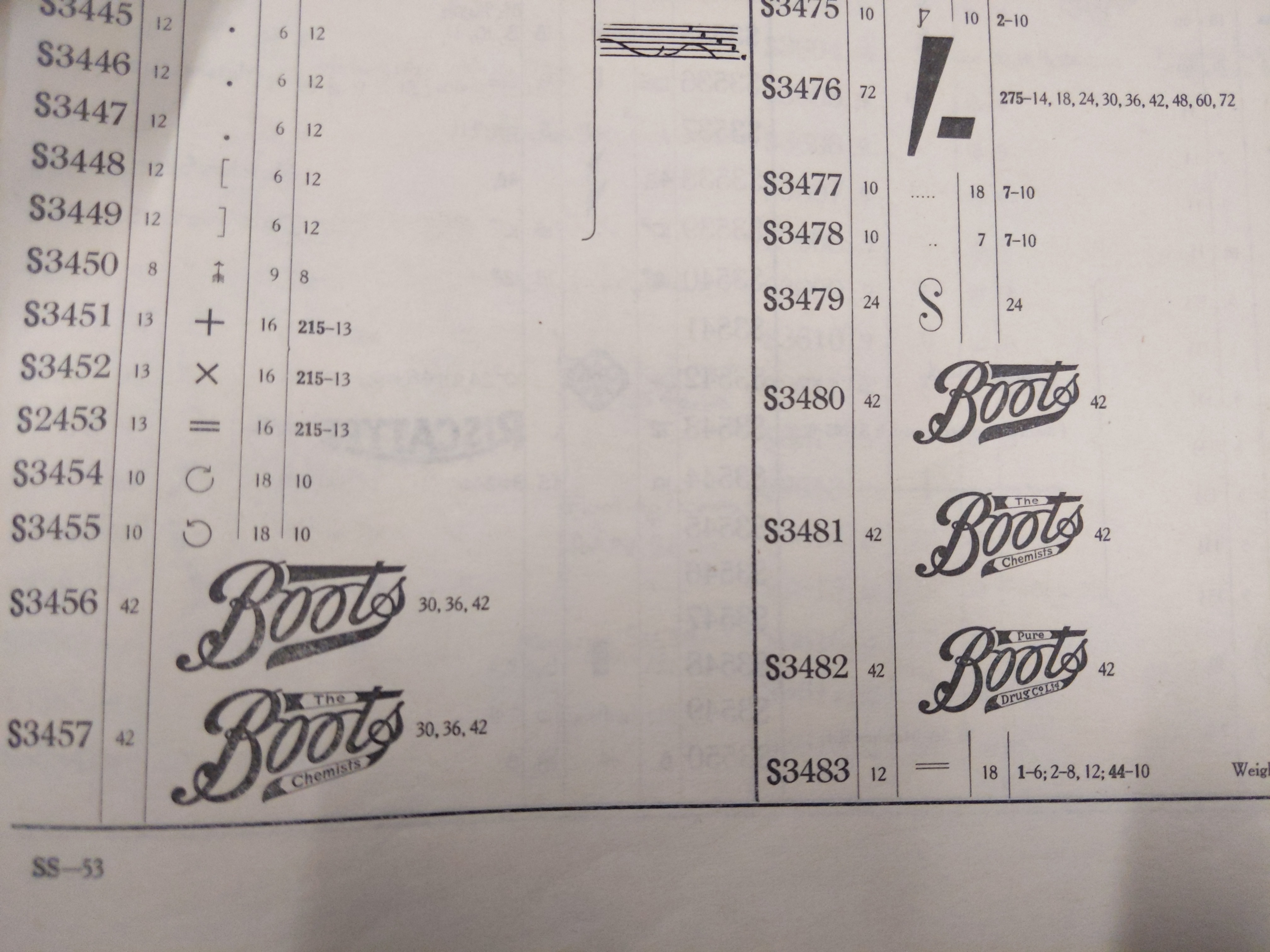
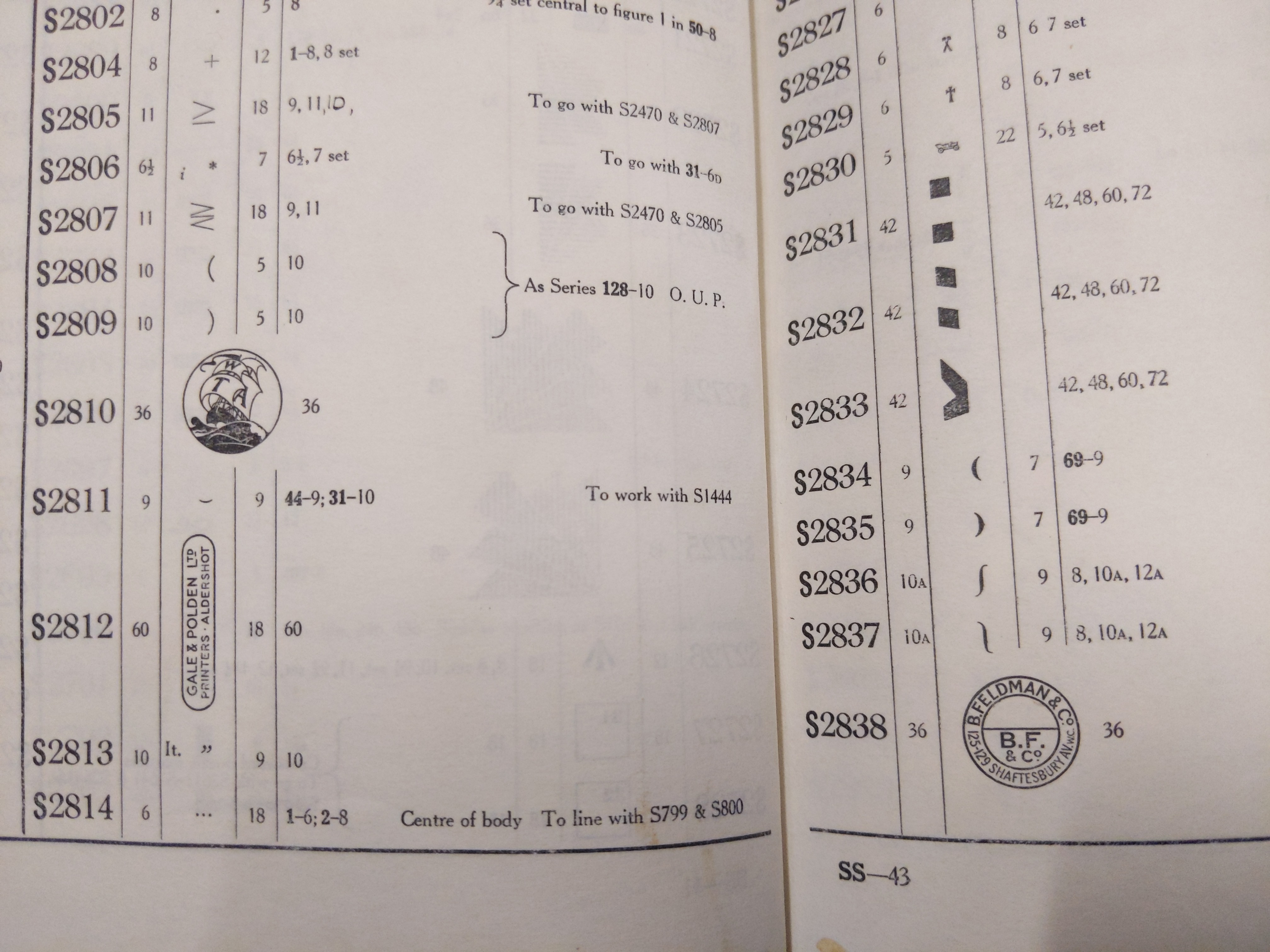
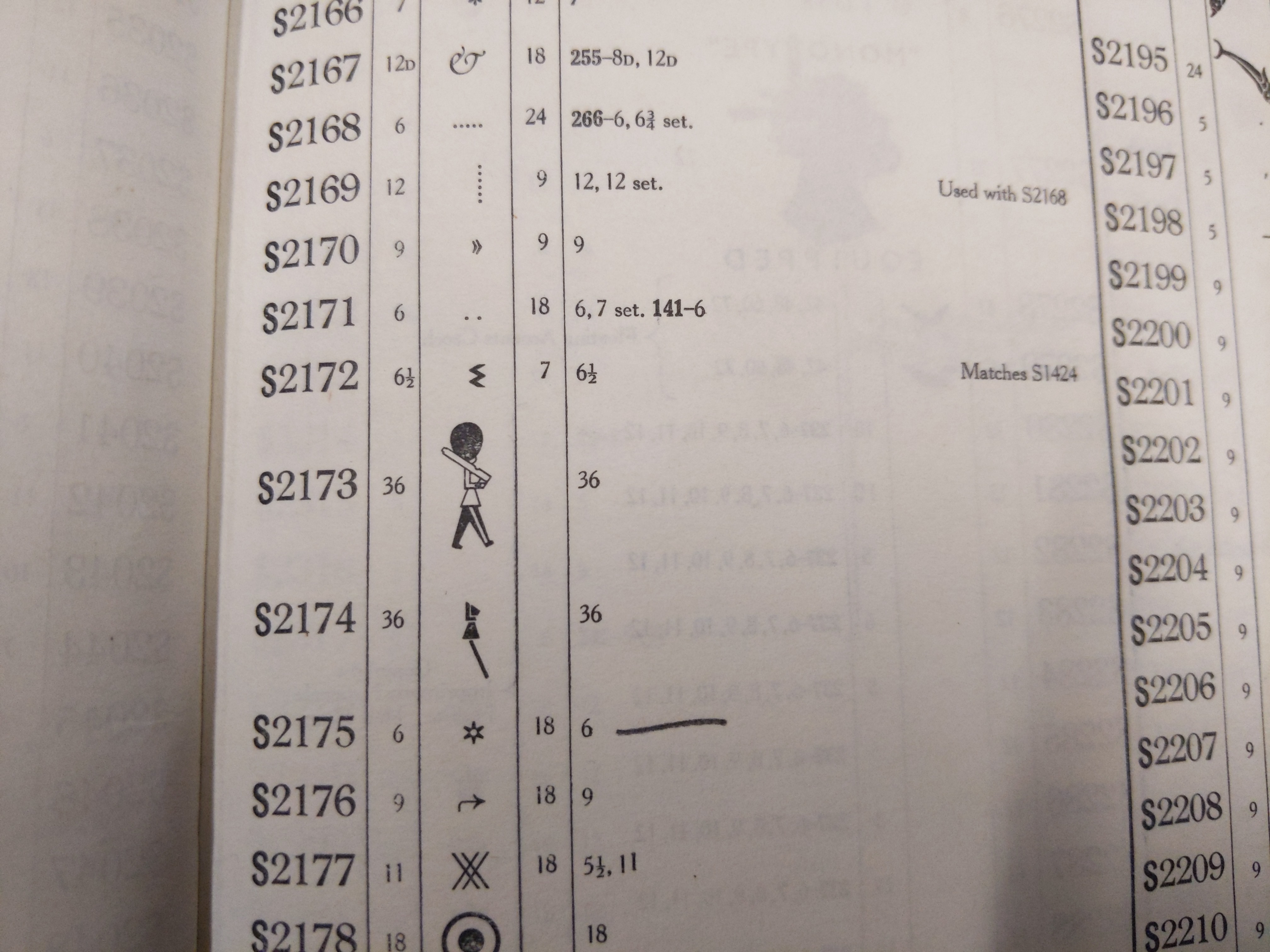
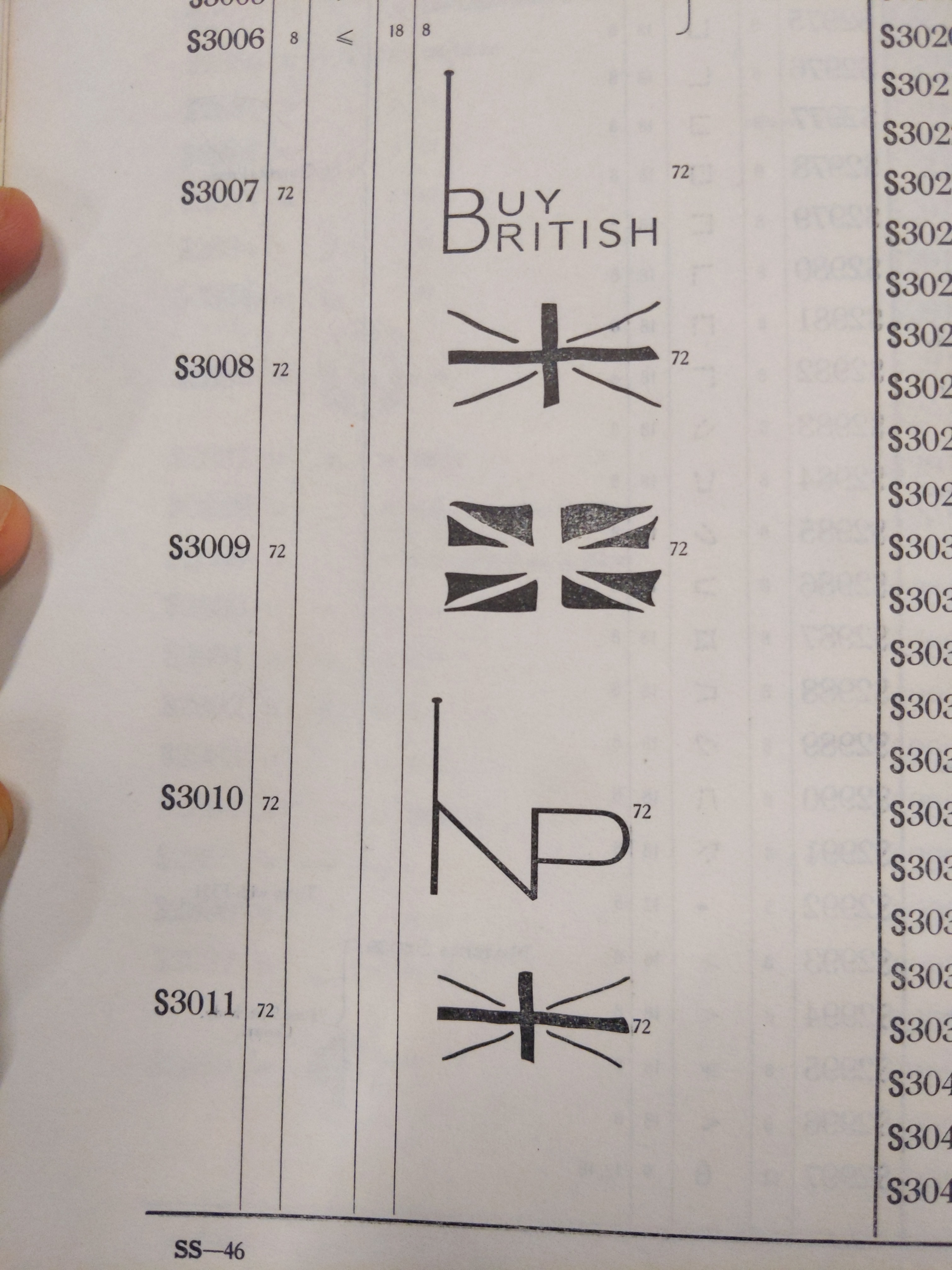
 Index to classified lists of Monotype special matrices
Index to classified lists of Monotype special matrices
.jpg) Front cover of Arrows & Shafts booklet, dated 10-66
Front cover of Arrows & Shafts booklet, dated 10-66
 interior.jpg) Interior of Arrows & Shafts
Interior of Arrows & Shafts


 S4182
S4253
S4521
S4182
S4253
S4521
 front.jpg) Front page of Arrows & Shafts, dated 12-54
Front page of Arrows & Shafts, dated 12-54
 back.jpg) Back page of Arrows & Shafts
Back page of Arrows & Shafts
.jpg) Front cover of Arrows & Shafts booklet, dated 1-63
Front cover of Arrows & Shafts booklet, dated 1-63
 interior.jpg) Interior of Arrows & Shafts
Interior of Arrows & Shafts