Why: Because.
How: With great effort and time.
I’ve gone through so, so many iterations of this installation process because of various things that have gone irreversibly wrong. Luckily, this has all been on a VM, so nothing is truly irreversible (save for the overall entropy of the universe), but many mistakes were made, then remade (“testing”, they call it) to be sure of their causes. To note:
-
Don’t install with separate partitions; put everything in one partition. Otherwise, when you boot up, fsck does a lot of shouting and you do a lot of shouting of a word similar to “fsck”. I reinstalled thrice and on VMWare just to confirm that it was really the partitioning that was the issue.
-
The installation is reported to only take 2 GB so it might seem like a good idea to give the virtual disk just 4 GB, but the installation really takes a bit more than 2 GB and the formatted disk really has a bit less than 4 GB and you’ll be installing extra packages and themeing-related files, which means you’ll run out of space and be unable to log in after you reboot because you put everything in one partition. The recommended amount is 10 GB, but I’ve redone my installation with 8 GB because I’m on a laptop with an SSD with only ~40 GB remaining that I’m loath to use up.
-
VMDKs can’t be resized. I’d’ve had to clone the disk to VDI, enlarge the disk, then clone back to VMDK. Or reinstall it, which took less time and space.
One cosmetic issue: the guest screen doesn’t fill up the host screen when maximized. It needs VirtualBox guest additions, and a bit more video memory than the recommendation to be able to run fullscreen if you have a higher-resolution screen. The same happens in VMWare, but when I tried to install VMWare Tools I had the guest screen stuck in a corner. Not being able to figure this one out was mainly why I stuck with VirtualBox, though I had to convert my VMWare .vmx to .ovf using VMWare’s OVFTool.
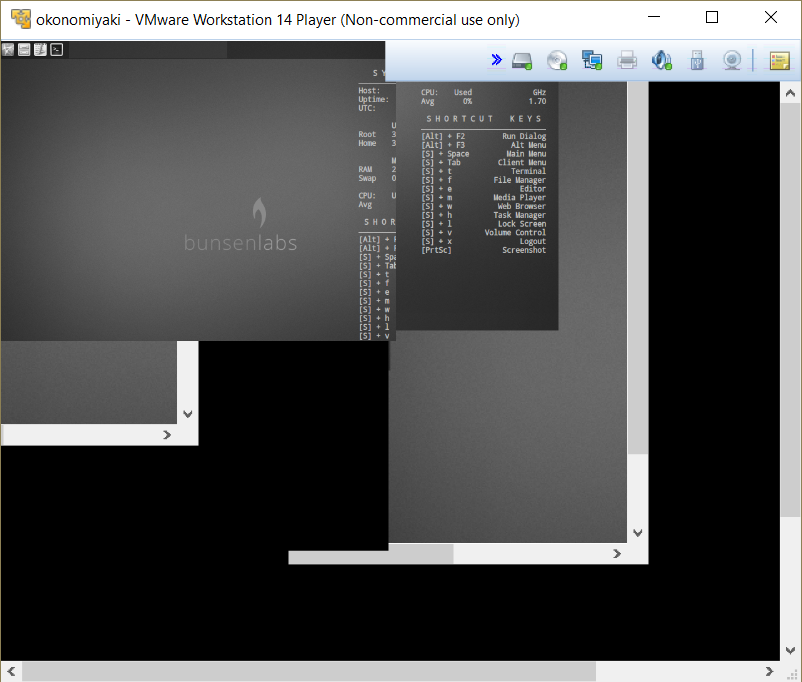
This isn’t a glitch in my screen capturing software, this is literally what I had to deal with
And now for the fun part: tweaking the UI! As usual, I went for a flat + dark theme using the following:
- Afterpiece (Openbox) ― double-click .odt to install
- FlatStudioDark (GTK3) ― paste folder into
~/.themes, then apply in Preferences > Appearance > Widget - Paper (icons) ― double-click .deb to install, then apply in Preferences > Appearance > Icon Theme
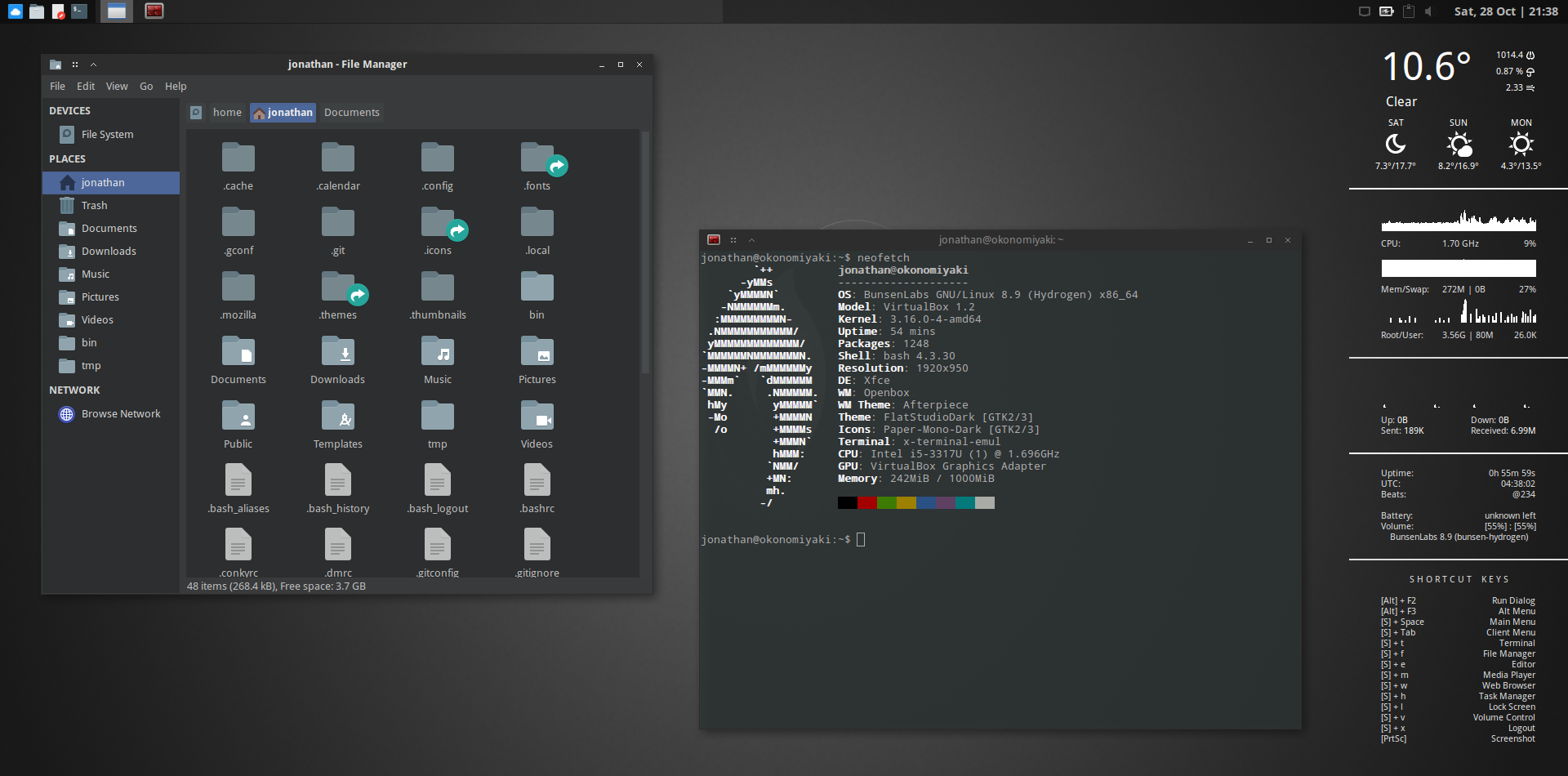
The Conky configuration is based off of this one and can be found here. In that repo are also configurations for Openbox and Tint2, whose defaults I’ve tweaked slightly with the following:
- Bindings for lowering, raising, and muting volume in
~/.config/openbox/rc.xml:
<keybind key=”XF86AudioLowerVolume”>
<action name=”Execute”>
<command>amixer set -D pulse Master 5%- unmute</command>
</action>
</keybind>
<keybind key=”XF86AudioMute”>
<action name=”Execute”>
<command>amixer set -D pulse Master toggle</command>
</action>
</keybind>
<keybind key=”XF86AudioRaiseVolume”>
<action name=”Execute”>
<command>amixer set -D pulse Master 5%+ unmute</command>
</action>
</keybind>
- Icons theme and clock format for Tint2 in
~/.config/tint2/tint2rc:
launcher_icon_theme = Paper
time1_format = %a, %d %b | %H:%M
I’ve also replaced the following default programs using GAlternatives found under System > Edit Debian Alternatives (where adding the same path with a new priority will update an existing entry’s priority):
- Geany -> VSCode (
/usr/bin/code), with custom settings (under File > Preferences > Settings)
{
"editor.scrollBeyondLastLine": false,
"editor.roundedSelection": false,
"editor.emptySelectionClipboard": false,
"workbench.startupEditor": "none",
"workbench.tips.enabled": false,
"telemetry.enableCrashReporter": false,
"telemetry.enableTelemetry": false
}
- Firefox ->
Opera BetaFirefox Developer Edition. Note that updates would need to be manually installed, so I’ve written a script (in$HOME/updatefirefox.sh) to do that for me. Theupdate-alternativesline isn’t necessary if it’s already been set through GAlternatives. This needs to be run withsudo -Ebecause a few of these commands require root and I want to preserve$HOME.
#!/bin/bash
TARBALL=~/Downloads/firefox.tar.bz2
URL="https://download.mozilla.org/?product=firefox-devedition-latest-ssl&os=linux64&lang=en-US"
wget -O $TARBALL $URL
rm -rf /opt/firefox
tar -xjvf $TARBALL -C /opt
update-alternatives --install /usr/bin/x-www-browser x-www-browser/opt/firefox/firefox 200
rm $TARBALL
Only a few final things to configure:
-
Adding
setxkbmap -option 'grp:ctrl_shift_toggle' 'ca(multix),us'to$HOME/.bashrcto set toggling between US and Canadian Multilingual Standard keyboard layouts with Ctrl-Shift; note that this is only run when a shell has started so a terminal will have to be opened before the changes are made -
Adding copy-paste functionality in Terminator (
~/.config/terminator/config):
[keybindings]
paste = <Control>v
copy = <Control>c
- Setting up SSH keys for GitHub using
ssh-keygenthengit remote set-url origin git@github.com:<user>/<repo>.git
And that should be it!


